|
|
摘要
LBM方法具有算法简单,空间、时间完全离散及粒子相互作用的局域性等优点使其适合分布式并行。OpenMP 编程模型是近些年来在共享存储系统基础上兴起的并行编程模型,目前在 Windows 和 Unix/Linux 平台上都有具体的实现,是一种非常适合共享存储系统的编程标准。利用 OpenMP 编写并行程序比MPI 开发程序更加简单,这是由于OpenMP 利用多线程技术,比 MPI 的多进程方式管理更加节省开销。本次计算使用OpenMP方法编写了并行程序。
关键词:顶盖驱动流 格子玻尔兹曼方法 OpenMP 并行
1. 顶盖驱动流的计算
1.1 顶盖驱动流简介
顶盖驱动方腔流是验证流体动力学问题计算方法的一个基准案例。该模型由一个二维方腔组成,其上壁具有切向速度,其他三个壁面速度为零。方腔的上边界以一个恒定速度水平右移,而其他三个边界则保持静止不动。其基本特征是:流动稳定后,方腔的中央有一个一级大涡出现,而在左下角和右下角会分别出现一个二级涡。当雷诺数Re超过一临界值后,在方腔的左,上角还会出现一个涡。这些涡的中心位置是Re数的函数。Re数的定义为Re=LU/v,式中L是方腔的高度(宽度),U是顶盖的移动速度,v是运动黏度系数。图1.1是顶盖驱动流模型示意图:
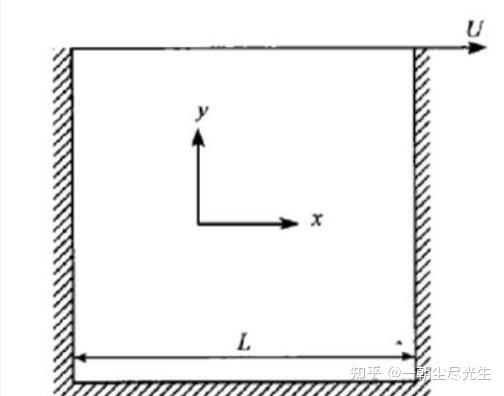
图1.1 顶盖驱动流模型示意图
1.2 顶盖驱动流计算方法
本次计算是在 Linux 系统下,用格子Boltzmann方法计算顶盖驱动方腔流,数值计算的程序使用C++语言编写。
1.2.1 格子Boltzmann方法简介
流体流动及过程中的特性可以从三个层面加以描述,图1.2指出了流体模拟的不同层面的示意图。
格子玻尔兹曼(LBM)方法[1]避免了传统CFD方法求解流体力学方程的复杂求解及低精度,通过介观的方法避免了粒子法存在的噪声问题,具有很强的物理基础:Boltzmann方程,可以很好的将微观粒子的动力学与宏观流体规律相结合,同时具有较好的精度。

图1.2 流体模拟的不同层面示意图
由于本文的重点不在LBM方法上,这里对LBM方程的离散与还原成宏观方程的过程就不做赘述了,这方面具体可在参考文献[2]中找到。先介绍Boltzmann模型的应用,一个完整的Boltzmann模型通常由三部分组成:格子(离散速度模型),平衡态分布函数以及分布函数的演化方程。 DdQm(d维空间,m个离散速度)系列模型是Boltzman方法的基本模型,本次计算采用了D2Q9模型。D2Q9模型的参数如图1.3所示。

图1.3 D2Q9模型的参数示意图
格子Boltzmann方法计算的具体步骤(不考虑外力的作用)如图1.4所示[3]:

图1.4 格子Boltzmann方法计算的具体步骤
从图1.4中可以看出,LBM方法最重要的步骤包括:设定正确的初始条件与边界条件(在三面固定壁面上使用回弹边界条件)、选择合适的格子玻尔兹曼模型,碰撞步与迁移步的正确实现等。
一次计算步骤完成后,计算宏观量并判断是否收敛,若计算收敛,则输出计算结果;否则
继续进行下一次碰撞直到收敛为止。
1.2.2 LBM程序参数的设定
LBM计算的程序使用C++语言编写,程序文件如图1.5所示:

图1.5 程序文件示意图
其中D2Q9Const.h中定义了D2Q9模型的参数,functions.h中声明了functions.cpp中定义的子函数,在主程序main.cpp按照计算步骤调用了LBM计算的相关子程序,并添加了计时函数进行运行程序耗时的计算。
程序的输入文件为input.txt,其中设定计算的雷诺数为 5000、计算网格为 1024*1024
流场初始密度为2.7,顶盖驱动速度U为0.1。
程序每10000步输出一次,将计算的方腔流流场数据输出到控制台,等到收敛的误差小于1e-10时,将流场信息输出到.plt文件中,此时程序运行结束。
程序最终的输出文件采用 Tecplot 格式,输出计算的信息包括流场的速度、密度、流函数等。最终能够使用Tecplot软件绘制出流线图和密度分布云图。
2. OpenMP并行计算
LBM方法具有算法简单,空间、时间完全离散及粒子相互作用的局域性等优点使其适合分布式并行。OpenMP 编程模型是近些年来在共享存储系统基础上兴起的并行编程模型,目前在 Windows 和 Unix/Linux 平台上都有具体的实现,是一种非常适合共享存储系统的编程标准。利用 OpenMP 编写并行程序比MPI 开发程序更加简单,这是由于OpenMP 利用多线程技术,比 MPI 的多进程方式管理更加节省开销。因此,OpenMP 已成为共享存储编程模型事实上的标准。本次计算使用OpenMP方法编写了并行程序。
2.1 OpenMP 介绍
OpenMP是共享存储编程模型的标准,是基于线程的并行编程模型。一个共享存储的进程由多个线程组成,OpenMP就是基于已有线程的共享编程范例;另外,OpenMP是一个外部的编程模型,而不是自动编程模型,它能够使程序员完全控制并行化[4]。
在共享内存并行程序时,采用的标准模式是Fork-Join的方式。如图2.1所示,程序开始只有一个主线程,程序中的串行部分都由主线程执行,并行部分通过派生从线程来执行;但是如果并行部分没有结束是不能执行串行部分的。从图2.1中可以看出,OpenMP并行执行的程序需要全部结束后才能执行后面的串行部分程序[5]。
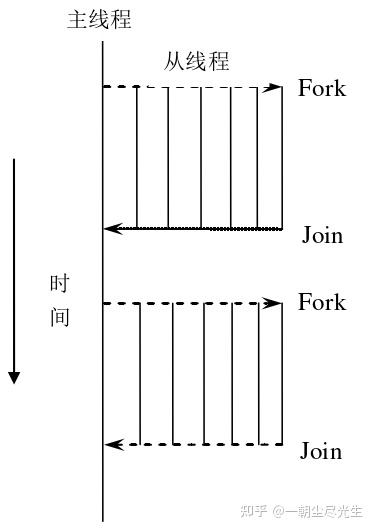
图2.1 OpenMP并行程序线程示意图
OpenMP 线程之间的数据交换是通过共享内存来实现的,这需要把共享变量存放在各线程都能访问到的共享存储区。同时还应允许通过私有化方式来说明,使各个线程可分别维护自己的私有变量。如图2.2所示,多个处理器通过共享内存来进行数据互通和交换。

图2.2 共享存储模型示意图
2.2 OpenMP计算硬件环境
本文进行研究的并行计算环境是在个人计算机中安装的Ubuntu虚拟机,在Ubuntu中安装了gcc version 7.5.0环境来编译运行C++程序。
计算机的CPU是第 12 代英特尔® 酷睿™ i7-12700H处理器,基频为2.70 GHz,睿频可达 4.70 GHz,共14核20线程,Linux环境的操作系统为Ubuntu 18.04。
2.3 OpenMP程序设计
在 OpenMP平台上,并行线程的创建、同步、负载平衡和销毁工作都是自动完成,从而为编写多线程并行计算程序提供了一种简便方法。
在OpenMP程序中,最主要的是编译指导语句,它指示编译器如何将串行程序转化成并行程序。一条编译指导语句由directive(命令,也叫指令)和clause list(子句列表)组成。以C/C++为例,OpenMP编译指导语句的格式为: #pragma omp parallel [clause[[,]clause]…] new line 例如对于如下语句, #pragma omp parallel private(i,j) parallel是命令,private是子句。
#pragma omp parallel 和其它指导语句合并就能变成相应的并行执行方式。常用的主要有 for 循环并行和功能并行(区段并行)两种方式,即在需要并行的程序段前加入#pragma omp parallel for 和#pragma omp parallel sections 进行编译指导处理。需要注意的是在 for 循环中不能包含允许循环退出的语句,如语句 break、return、exit、goto 以及此类转移到循环体外的标记。
本次计算在主程序读取输入文件后就使用omp_set_num_threads(CORES);语句设定并行的核数,CORES在头文件后用宏定义定义,可以定义为#define CORES 8或4或2或1。
OpenMP 并行程序的设计主要靠 parallel 指导语句来定义,即是在需要并行执行的程序区段前面插入#pragma omp parallel 指导语句,编译器在对程序进行编译时就会在此处自动的创建多个线程。在子函数定义文件functions.cpp中在for 循环程序段前加入#pragma omp parallel for子句。值得注意的是在 for 循环中不能包含允许循环退出的语句,如语句 break、return、exit、goto 以及此类转移到循环体外的标记。
OpenMP的变量有共享(shared)和私有(private)两种类型。在并行区域外是同名原始变量,而在并行区域内的共享变量是对并行区域外的同名原始变量的引用;并行区域内的私有变量则是每个线程(主线程可能不包括)会各自创建并行区域外同名原始变量的一个副本。并行区域内各个线程实际操作的私有变量都是自己的副本,因此不会出现数据竞争的情况。如果访问共享变量时多个线程同时访问存在写操作,则会出现数据竞争现象。
针对共享变量的问题,将for 循环程序段前的并行字句改为#pragma omp parallel for schedule(static) shared(共享的变量),将会被其他语句中调用的变量设置为共享的(shared)。
3. 并行计算结果
3.1 LBM程序计算结果与分析
采用OpenMP的8线程并行运行程序,尽量减少程序的运行时间,最终在第14480000步时误差收敛到了1e-10,程序结束运行,并输出了雷诺数为 5000、计算网格为 1024*1024的流场信息文件。
文件中的数据包含:VARIABLES = "X","Y","U","V","rho","p","PSI","Vorticity","Fd","cd"。
这些变量分别表示:X,Y的坐标,X,Y方向的速度分量,密度,压力,流函数,涡量,动壁面阻力和阻力系数。
3.1.1 流场分布云图对比
将输出文件的云图与参考文献[6]中的云图进行对比,首先进行Re=5000时流函数的对比,如图3.1所示:
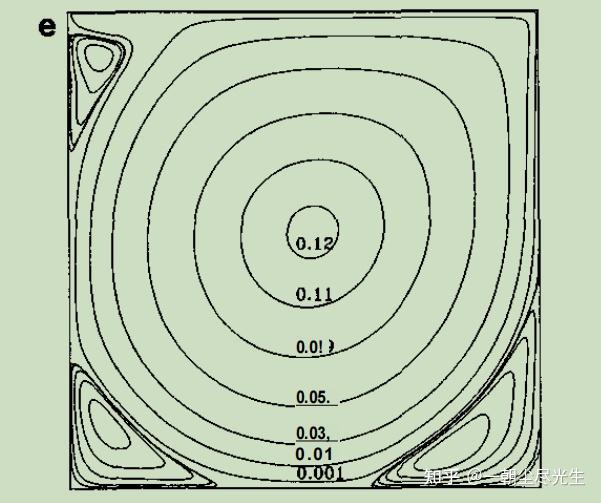
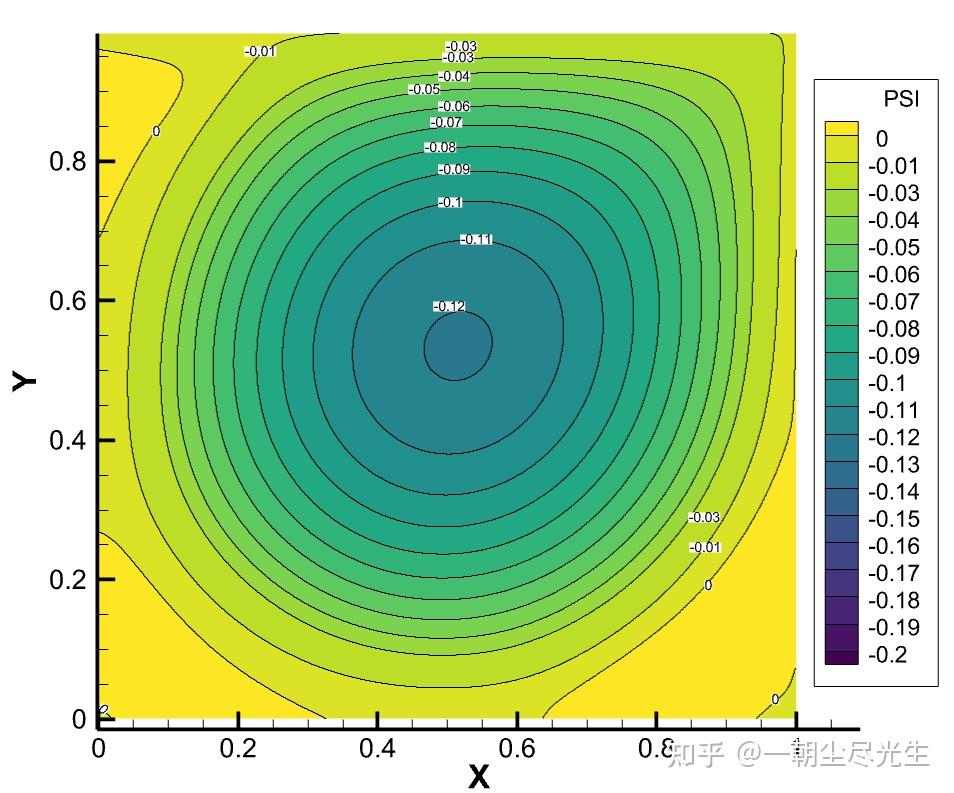
图3.1 Re=5000的流函数对比图
图3.2为Re=5000时流场涡量等值线的对比图:

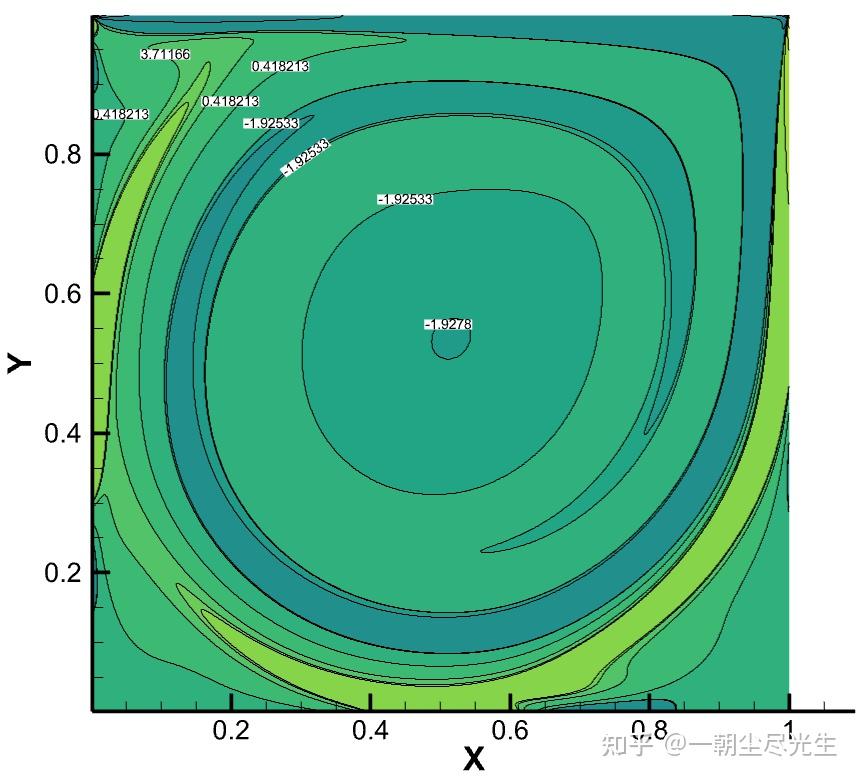
图3.2 Re=5000的涡量等值线对比图
图3.3为Re=5000时流场压力的对比图:

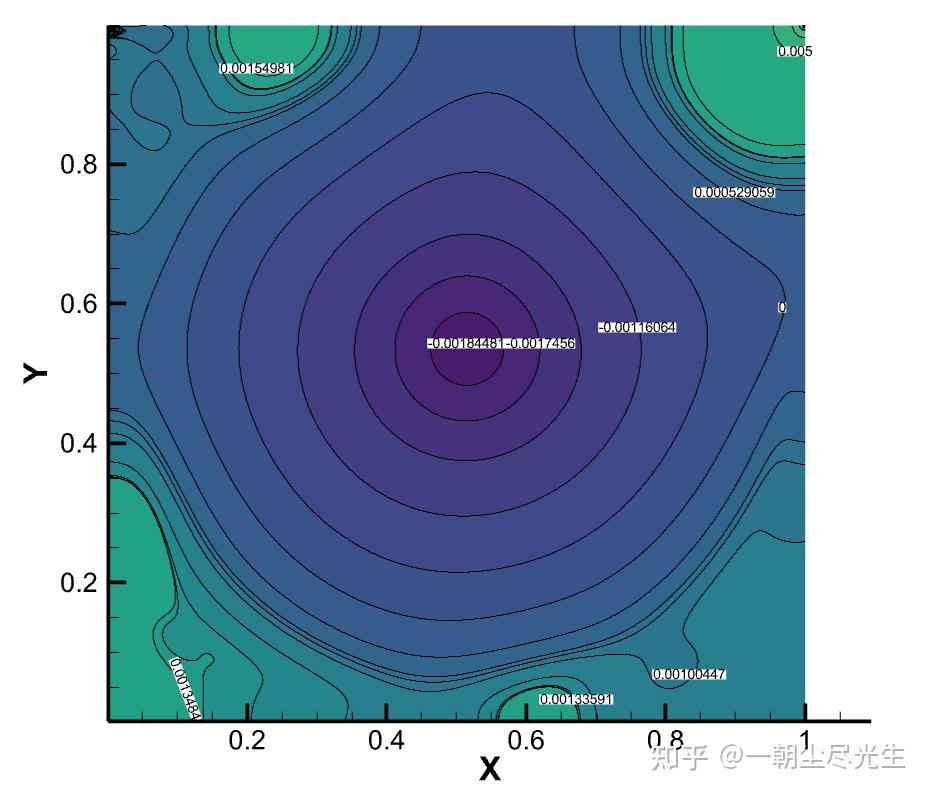
图3.3 Re=5000的压力等值线对比图
3.1.2 流线图与密度分布云图
流场的密度分布云图如图3.4所示:
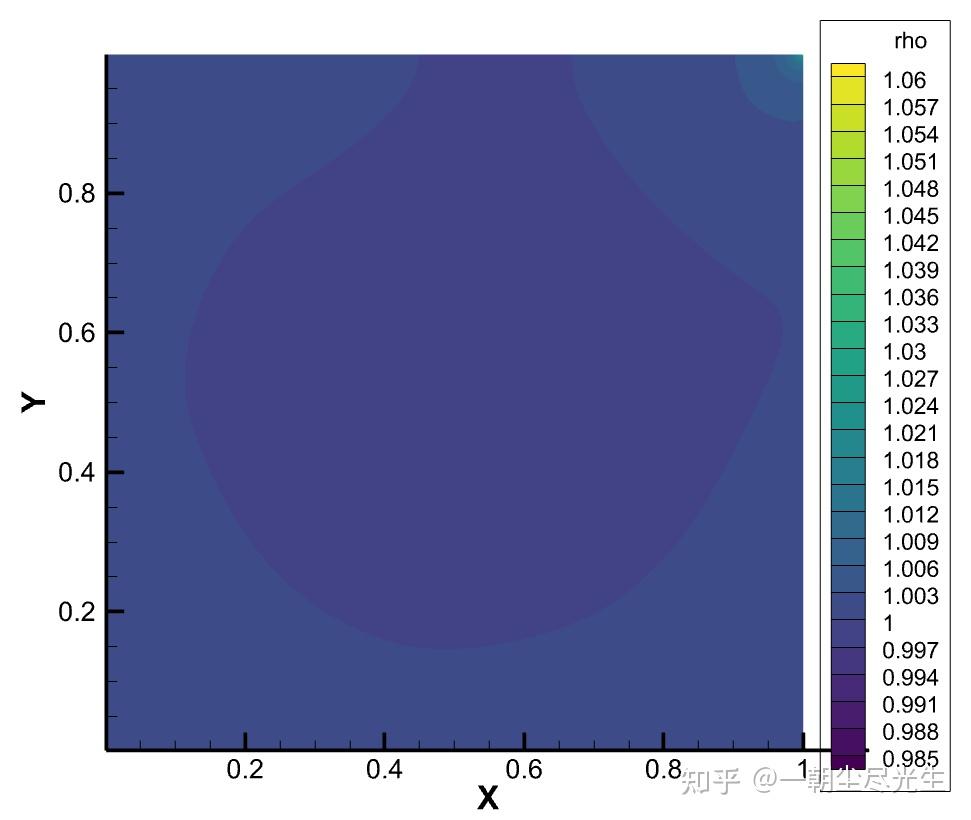
图3.4 Re=5000的压力密度分布云图
流场的流线图如图3.5所示:

图3.5 Re=5000的流线图
观察图3.5并结合文献[2]中其他雷诺数的流线图可以得出结论:
当Re数较小时(Re<=1000),方腔中只出现三个涡:一个位于方腔中央的一级涡和一对位于左下角和右下角附近的二级涡。当Re= 2000时,在左上角出现第三个二级涡。当Re数上升至5000时,在右下角出现了一个三级涡。从图中还可以看到,随着Re数的增加,一级涡的中心向方腔的中央位置移动。
从流线图中可以看出,该程序的模拟结果与文献的结果吻合得很好。
3.1.3 速度型分布曲线对比
过中心的水平截面的 Y 方向速度型对比如图3.6所示:
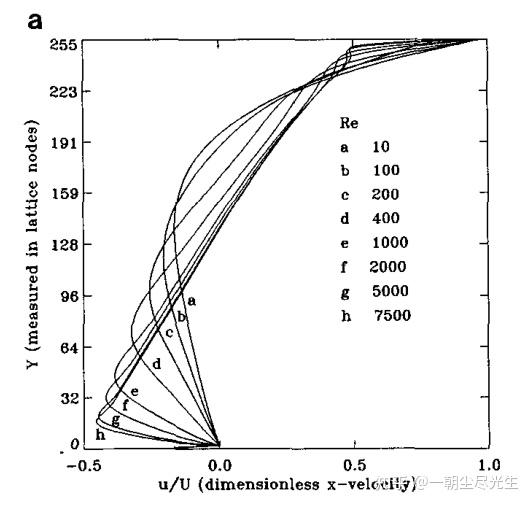
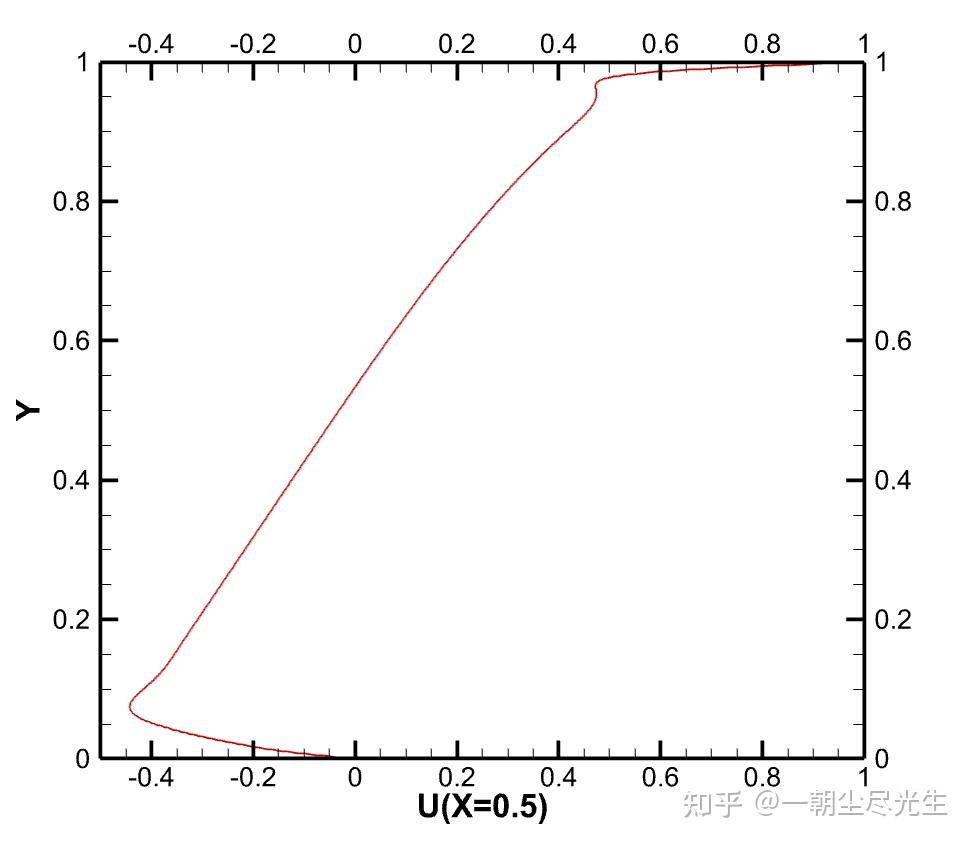
图3.5 过中心的水平截面的 Y 方向速度型对比图
过中心的垂直截面的X方向速度型对比如图3.7所示:
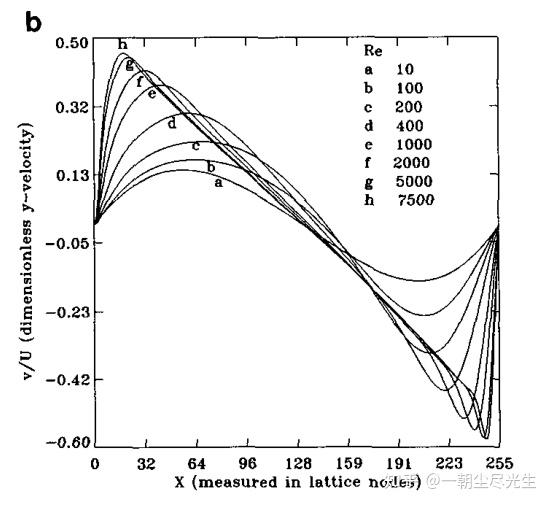

图3.6 过中心的垂直截面的 X方向速度型对比图
3.1.4 LBM计算结果分析
从流场参数的分布云图和几何中心速度型的对比中可知,Re=5000时流场的LBM计算结果与文献结果十分吻合,计算得到的数据基本正确。
3.2 并行计算结果与分析
3.2.1 并行计算性能定义
并行程序的实现是为了比串行程序更快,评判并行计算的基本定义有加速比和效率。加速比(speedup)是串行程序与并行程序执行时间之比,定义效率为加速比与使用的处理器数之比。
3.2.2 OpenMP并行计算结果
分别将程序设置成串行、2、4、8 核并行运行,输出并记录 10000 步的纯计算时间,输出的结果如图3.8所示。
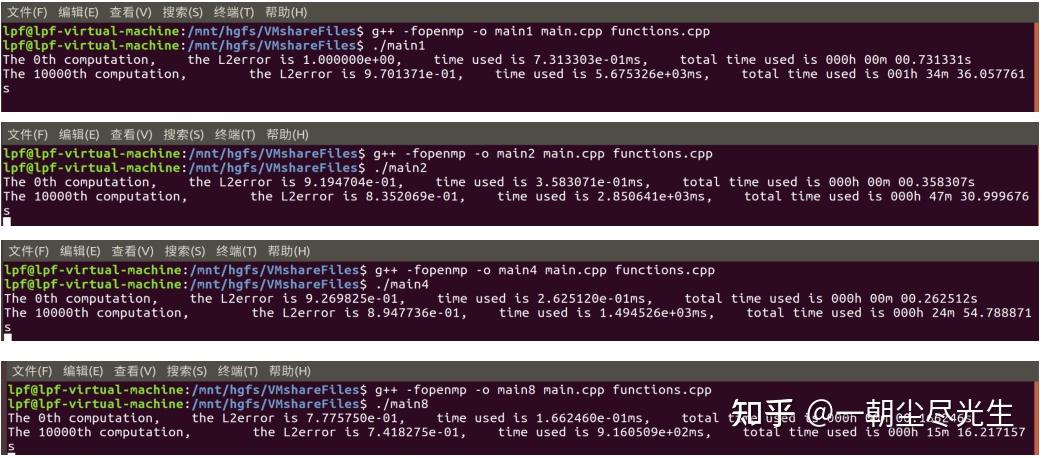
图3.8 计算时间输出结果图
这里需要注意的是串行源程序使用的计时函数在linux系统下去计时的话,计算出来的时间是所有核数计算时间的总和,而不是时钟时间,刚开始运行时出现了计时错误。
查阅资料[8]后可知在Linux系统下使用OpenMP的omp_get_wtime函数去计时,这样才是正确的。
根据3.2.1节中的计算公式将加速比和并行计算效率计算出来,并与计算时间一同记录在表1中。
表1 OpenMP并行计算结果
| 核数 | 1(串行) | 2 | 4 | 8 | | 10000步计算时间(秒) | 5676 | 2851 | 1495 | 916 | | 加速比 | 1 | 1.9905 | 3.796 | 6.1954 | | 并行计算效率 | 1 | 0.9953 | 0.949 | 0.7744 |
使用MATLAB软件绘制加速比和并行计算效率[9]与所用核数的关系的曲线,如图3.9和3.10所示:
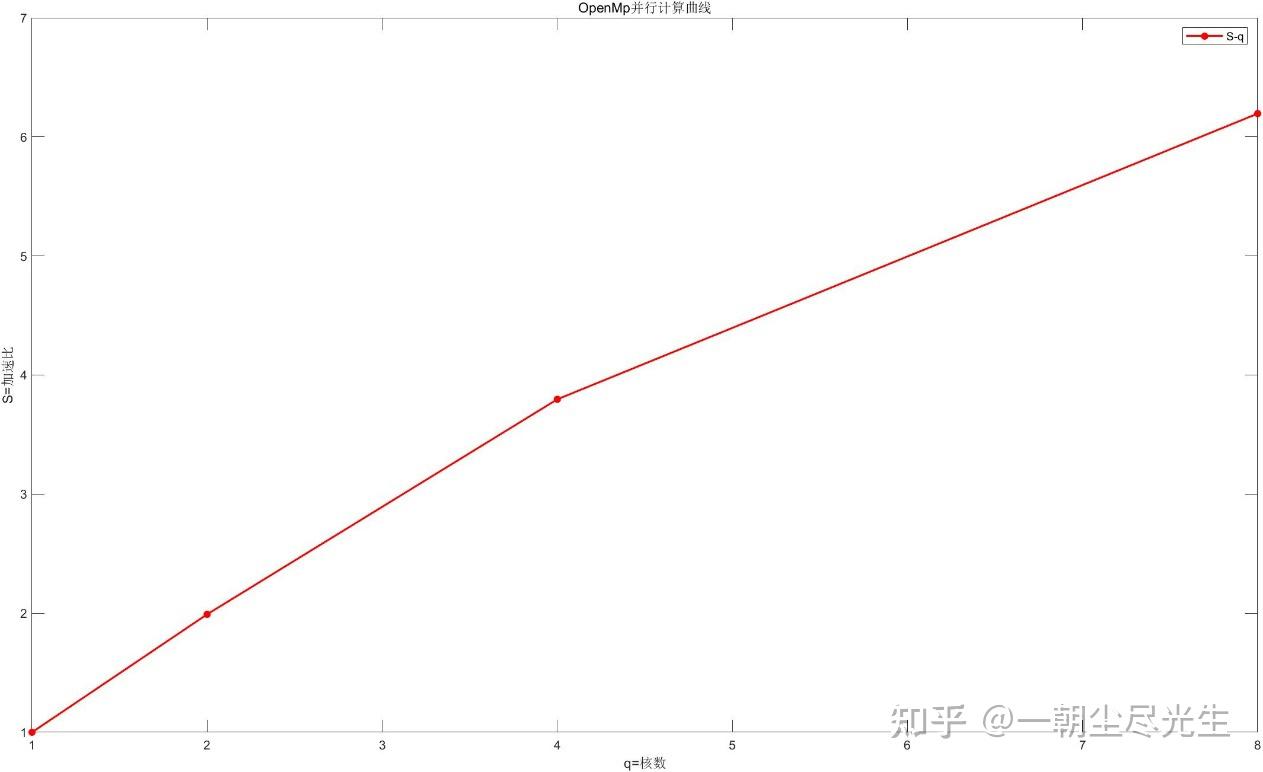
图3.9 加速比曲线示意图
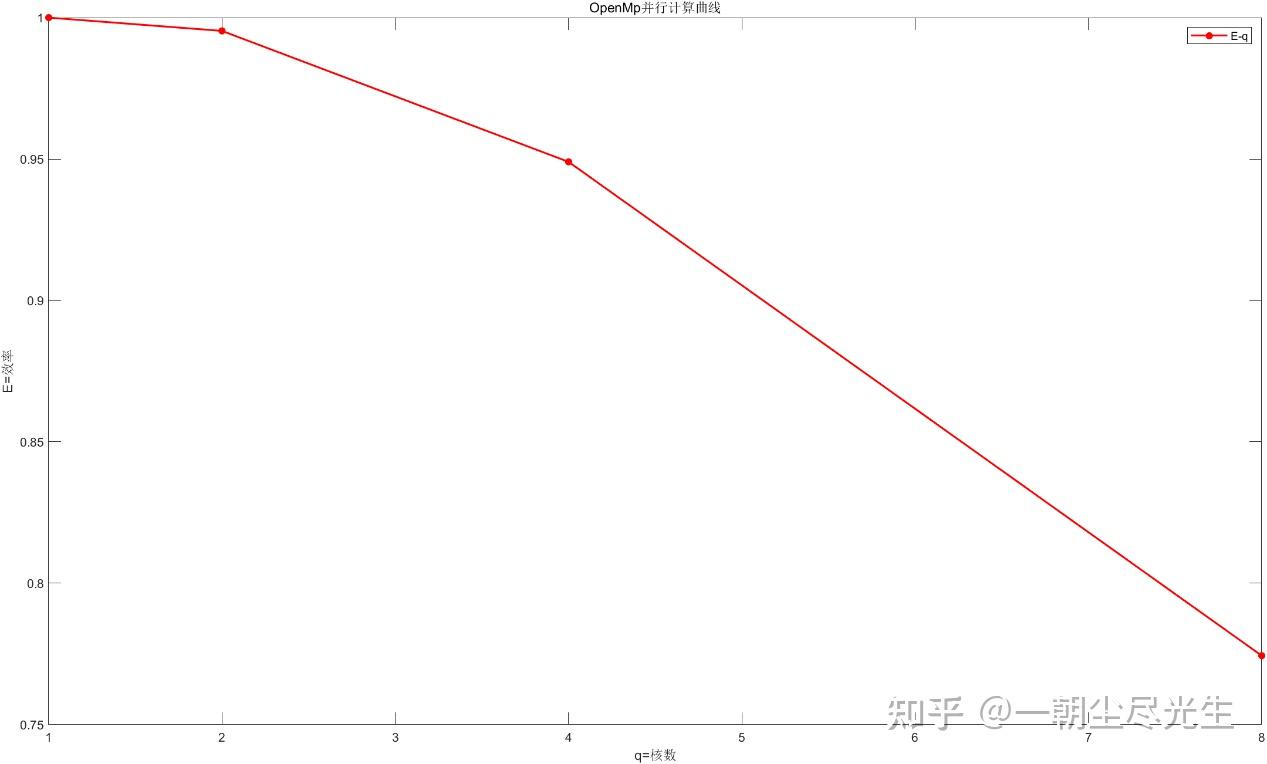
图3.10 并行计算效率曲线示意图
参考文献
如需代码可私 |
|