|
|
一、平衡小车控制原理
1、感性认识
平衡小车的控制与用手指控制木棍不倒的过程相似,人们通过眼睛观察木棍的倾角和倾斜的趋势(角速度),并用手指的移动来抵消,进而实现木棍直立(典型的负反馈机制)。同理,通过用陀螺仪代替人眼得到角度和角速度值,采用负反馈,从理论上讲,只要电机的速度足够大就能让电机控制小车移动,使得小车直立。
2、直立环
让小车直立是我们的根本目的,所以从直立环开始分析,从控制木棍不倒的过程中我们可以体会到:为了保持平衡,倾角越大,移动的速度就要越大,即:
u=k p^* \theta
但是,通过上述的控制还不能达到要求,因为物体都具有惯性,如果只采用上面的方式进行控制,当角度为0时控制器的输出仍为0, 但小车会因为惯性继续向前或向后倾斜,不断往复就会造成小车来回调整(超调与震荡),从高中物理单摆的运动中我们学到想要克服这种现象的产生,需要回复力,也就是与运动速度成正比且与运动方向相反的力使得小车最终停下来趋于稳定,即:
u=k p^* \theta+k d * \theta^{\prime}
事实上,这就是一个位置式的PD控制器。
3、速度环
直立环完成后还需要考虑一个问题,除了小车平稳不动以外,如果小车有一定的倾角并保持一个匀速运动此时,小车的角度同样不变,这同样也是一种“稳态”,但是这种稳态我们是不希望得到的,我们希望的是小车保持不动,即速度也为0,因此我们给速度也加一个闭环反馈与直立环一起构成一个串级PID控制。为了保证直立控制的优先,我们将直立环放在内环,速度环放在外环,为了克服编码器存在的系统误差,我们采用PI控制如图:
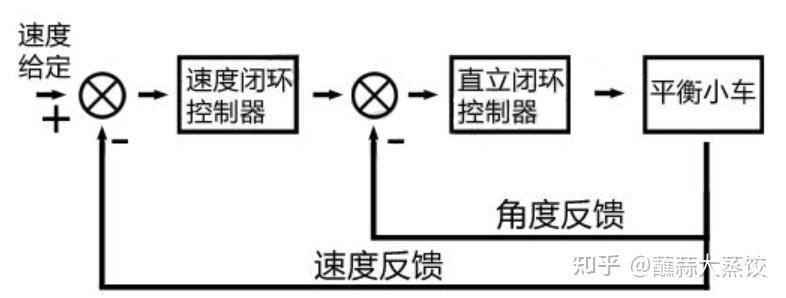
串级PID原理图
u_1=k p_1 * e(k)+k i_1 * \sum e(k)
将速度环与直立环的输出方程联立得到:
u=k p * \theta+k d^* \theta^{\prime}-k p\left[k p_1 * e(k)+k i_1 \sum e(k)\right]
根据输出方程可以将上面的算法转化成为:一个单独的负反馈的直立环 + 一个单独的正反馈的速度环,也就是大家常说的平衡车的速度环是正反馈的由来。如下图:
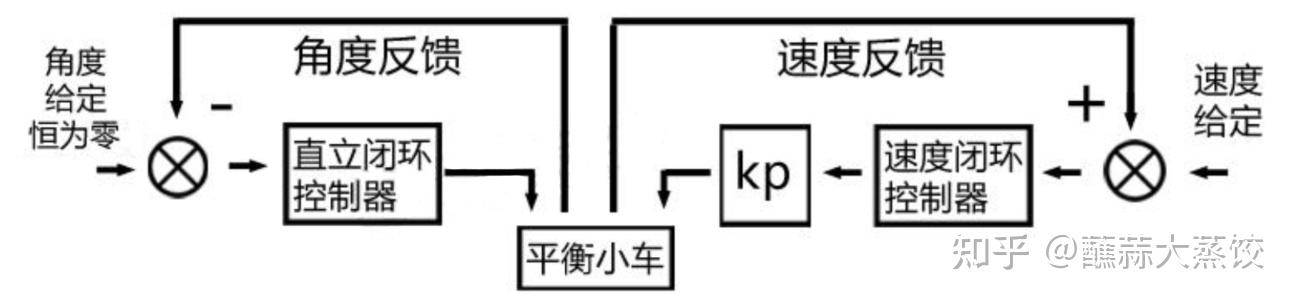
转化后的串级PID原理图
二、系统硬件组成
平衡小车主要由系统主控,小车底盘,编码器,电机,陀螺仪,电机驱动,电源模块组成,其系统框图如图所示。平衡小车用两个电机作为动力,并不断采集角度值、角速度值和编码器的值,并将其反馈给单片机主控,单片机经过计算后得到输出值,并控制驱动电机运动。
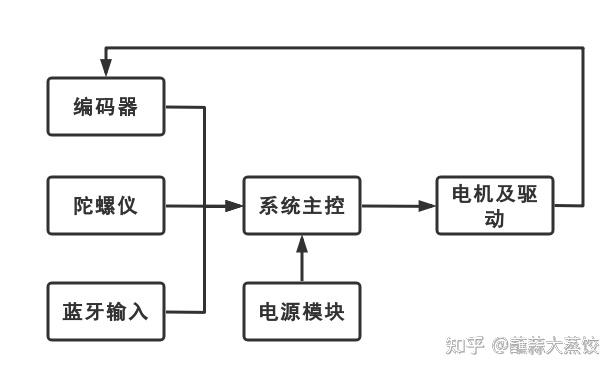
平衡小车系统框图
1、系统主控部分
主控使用STM32F103RCT6最小系统,STM32F103单片机是32位单片机,内部集成度高,拥有大量外部接口,运算速度高,能够满足问题中对数据的快速采集和处理需求。其硬件资源为:48KB的SRAM、256KB的FLASH、2个基本定时器、4个通用定时器、2个高级定时器、2个DMA控制器(共12个通道)、3个SPI、2个IIC、5个串口、1个USB、1个CAN、3个12位ADC、1个12位DAC、1个SDIO接口及51个通用IO口。
2、陀螺仪模块
陀螺仪模块采用WT61六轴陀螺仪,此六轴模块采用高精度的陀螺加速度计MPU6050,通过处理器读取MPU6050的测量数据然后通过串口输出,免去了用户自己去开发芯片复杂的I2C协议,同时精心的PCB布局和工艺保证了陀螺加速度计收到外接的干扰最小,测量的精度最高。
3、电机驱动模块
L298N是一种高电压、大电流电机驱动芯片。该芯片采用1脚封装。主要特点是:工作电压高,工作电压可达46V;输出电流大,瞬峰值电流可达3A,持续工作电流为2A;额定功率25。内含两个H桥的高电压大地啊牛全桥式驱动器,可以用来驱动直流电动机和步进电动机、继电器线圈等感性负载;采用标准逻辑电平信号控制;具有两个使能控制端,在不受输入信号在低电平压下工作;可以外接检测电阻,将变化量反馈给控制电路使L298N芯片驱动电机,该芯片可以驱动一台两相步进电机或四相步进电机,也可以驱动两台直流电机。
4、蓝牙模块
HC-05蓝牙模块,是一种集成蓝牙功能的PCBA板,用于短距离无线通讯,用户可以通过AT指令对其设备名,连接密码,波特率等参数进行修改,方便快接使用灵活。在这里其主要功能是实现运动模式选择、确定、模式启动、PID参数调试、波形输出、画圆运动半径选择。
5、电源模块
采用LM2596SDC-DC直流可调降压稳压电源模块,此模块使用优质的LM2596芯片,效率高(最高92%),发热量小,能很轻松带3A(短时间)电流,长时间工作建议在2A以内的电流使用,同时加上散热(10W以上输出)。本系统从开关电源处的12V电压经过此模块稳压到5V供给电机,单片机以及其他模块的电源使用。
三、外设配置
1、软件准备
- STM32Cube:STM32Cube是一个全面的软件平台,包括了ST产品的每个系列。对于新的产品设计,强烈推荐使用STM32Cube来加速你的开发过程,并为以后的产品平台移植打下良好的基础。
- Keil-uVision5:Keil-uVision5是一款专业的单片机开发工具,通过这款软件可以帮助单片机开发人员轻松快发单片机。
- 匿名上位机:匿名上位机为了提供给大家一个更好的调试工具,便于我们观察输出波形,以及对参数的整定。
2、 时钟设置
将外部晶振作为外部高速时钟和低速时钟。
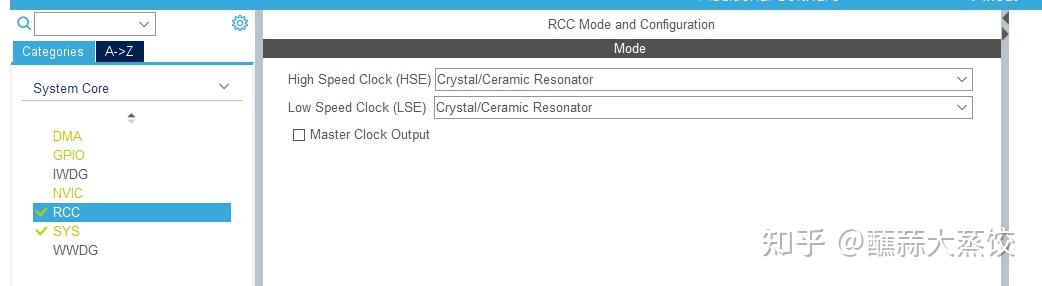
时钟选择
将时钟频率设置成最高时钟72M。
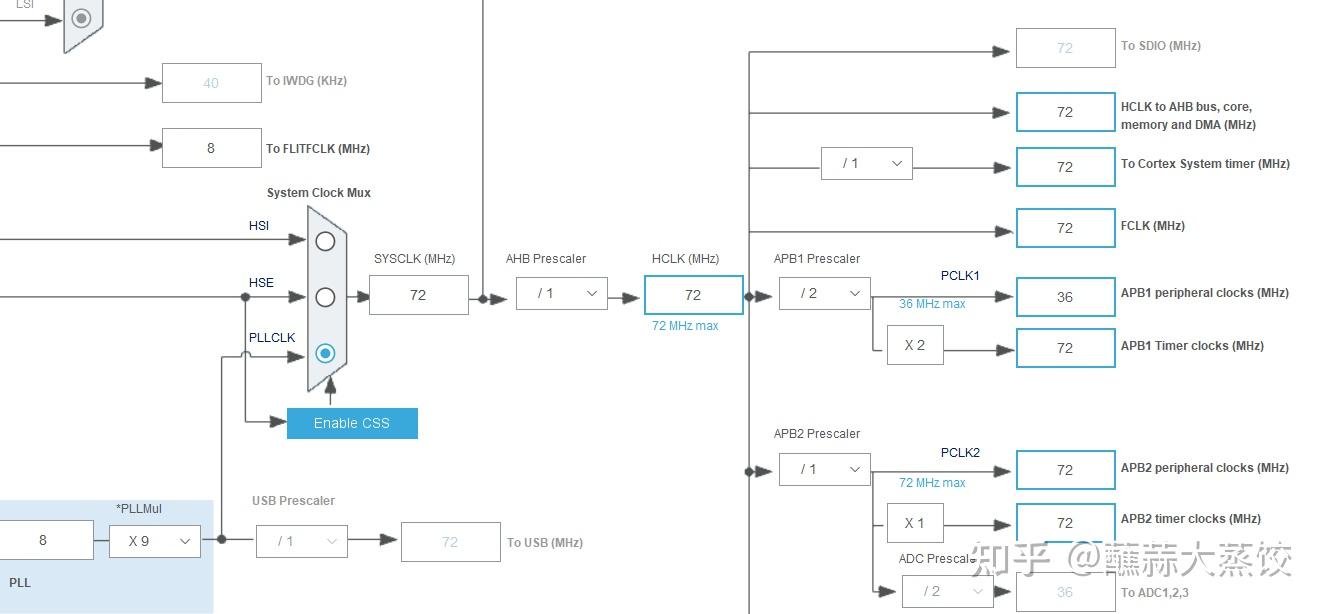
时钟配置
3、 调试方式设置
调试方式选择为SWD调试
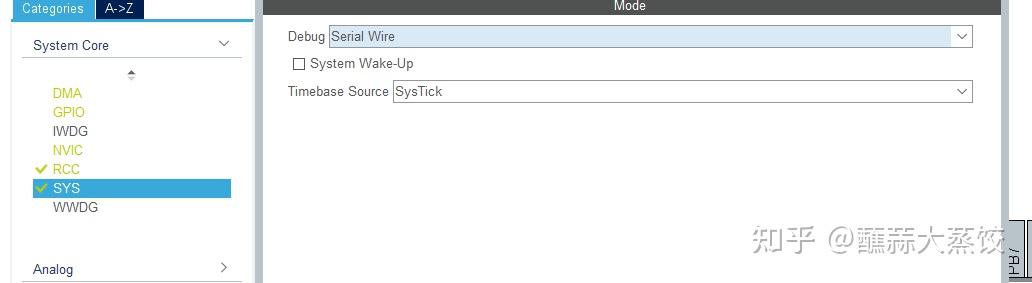
调试方式选择
4、定时器设置
配置基本定时器,选择TIM1,在TIM1配置中选择内部时钟作为时钟源,查看数据手册或者查看代码可以知道TIM3是挂接到APB2时钟线上。
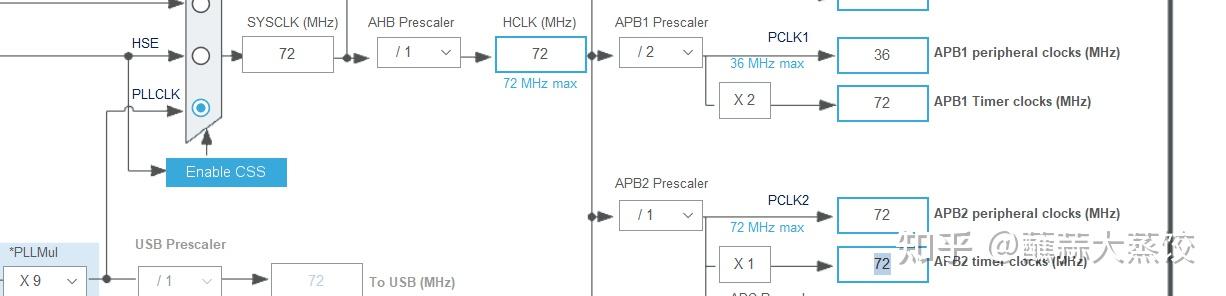
时钟树
由于TIM1是挂在APB2总线上,查看时钟树我们知道APB2当前频率为72MHz,我们希望5ms发生一次中断来对风力摆进行控制,把预分频系数设为7200-1,自动重装值设为50-1,得到的中断频率即为
\frac{72000000}{7200 \times 50}=200 \mathrm{HZ}
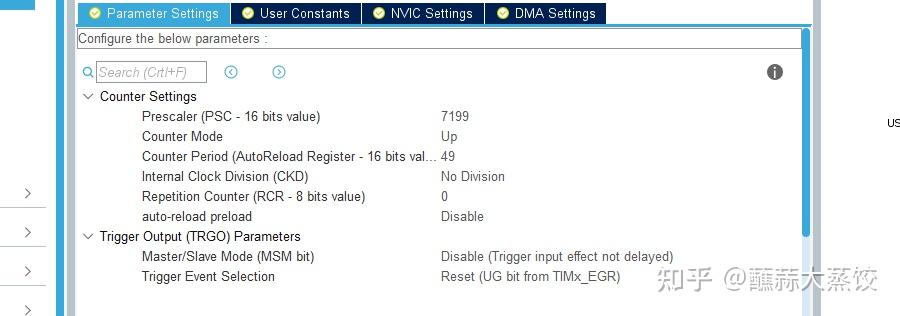
TIM参数设置
完成参数设置后开启定时器中断。
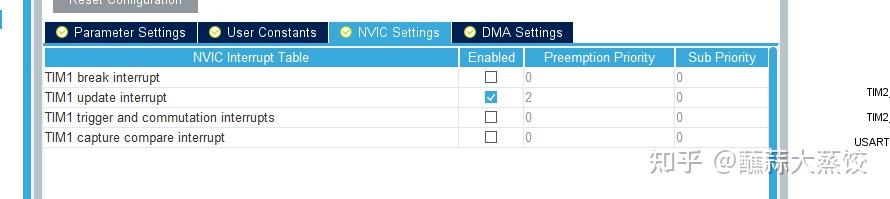
TIM中断设置
定时器PWM输出配置,选择定时器TIM4,将其4个通道设置成PWM输出。

TIM4PWM参数设置
将TIM4定时器的自动重装载值设置成5000-1,即PWM的脉宽设置为0到5000。

TIM4参数设置
5、串口设置
串口设置,选定USART2,串口配置设置波特率为115200Bits/s。传输数据长度为8Bit。奇偶检验无,停止位1。其他参数默认。USART1除波特率设置为9600外,其他参数设置与USART2相同。

USART2参数设置
开启USART2中断服务。

USART2中断设置
给USART2添加DMA接收请求并设置成高速循环模式。
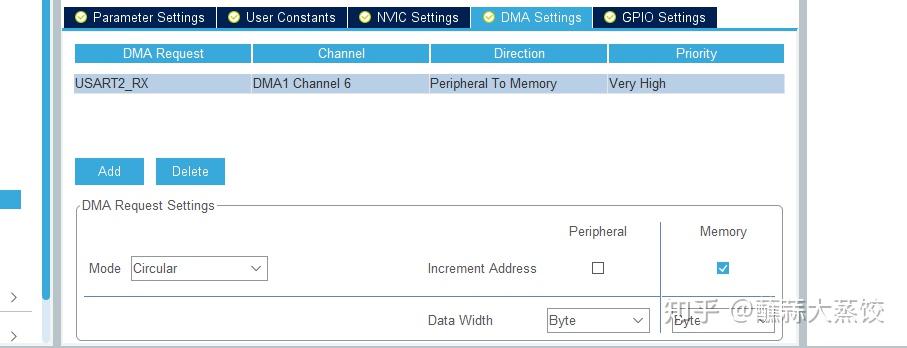
USART2DMA设置
6、编码器模式设置
将定时器2和3设置成编码器模式。

编码器模式设置
7、 单片机引脚配置图
完成上述单片机外设配置后,得到引脚视图。
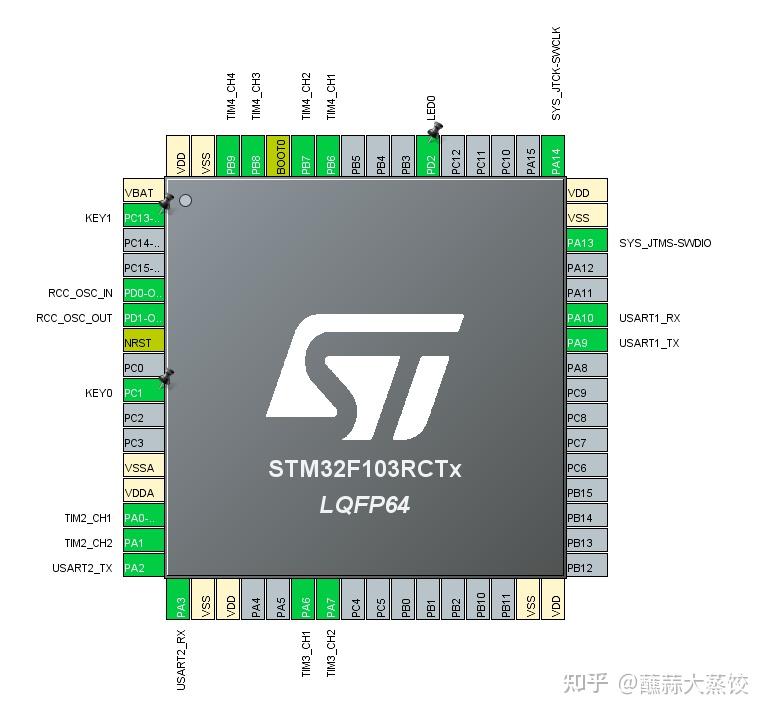
单片机引脚视图
四、基础程序设计
1、 陀螺仪读取程序
通过查阅WT61陀螺仪以及L298NS的产品手册,编写串口2的接收中断程序和电机驱动程序。
if(huart->Instance == USART2)
{
RxBuff[Rx_Count++]=RxByte;
if(RxBuff[0]==0x55)
{
if(RxBuff[1]==0x53)
{
Angle_X = ((short)(RxBuff[3]<<8|RxBuff[2]))/32768.0*180;
Angle_Y = ((short)(RxBuff[5]<<8|RxBuff[4]))/32768.0*180;
Angle_Z = ((short)(RxBuff[7]<<8|RxBuff[6]))/32768.0*180;
}
else if(RxBuff[1]==0x52)
{
Velocity_Angle_X = ((short)(RxBuff[3]<<8|RxBuff[2]))/32768.0*2000;
Velocity_Angle_Y = ((short)(RxBuff[5]<<8|RxBuff[4]))/32768.0*2000;
}
else if(RxBuff[1]==0x51)
{
Acc_Angle_X = ((short)(RxBuff[3]<<8|RxBuff[2]))/32768.0*16*9.8;
Acc_Angle_Y = ((short)(RxBuff[5]<<8|RxBuff[4]))/32768.0*16*9.8;
Acc_Angle_Z = ((short)(RxBuff[7]<<8|RxBuff[6]))/32768.0*16*9.8;
}
}
else
{
Rx_Count=0;
}
if(Rx_Count>10)
{
Rx_Count=0;
}
while(HAL_UART_Receive_IT(&huart2,&RxByte,1)==HAL_OK);
}2、编码器读取程序
在定时器中断中获取编码器数值并清空即可得到每5ms编码器的脉冲数,用此数值可以当作小车电机的速度
enc1 = -(short)__HAL_TIM_GET_COUNTER(&htim2);
__HAL_TIM_SET_COUNTER(&htim2,0);
enc2 = (short)__HAL_TIM_GET_COUNTER(&htim3);
__HAL_TIM_SET_COUNTER(&htim3,0);3、低通滤波程序设计
为过滤掉陀螺仪得到数据中存在的干扰,本系统采用软件编程的方式实现低通滤波,即让低频的信号能正常通过,而超过设定临界值的高频信号则被阻隔和削弱。低通滤波的算法实现功能如下:
y(n)=q^* x(n)+(1-q)^* y(n-1)
其中y(n)为输出,x(n)为输入,y(n-1)为上一次输出值,q为滤波系数。取值范围为0-1。这里的滤波系数越小,滤波结果越平稳,但是灵敏度越低;滤波系数越大,灵敏度越高,但是滤波结果越不稳定,本系统选择滤波系数为0.7。
Encoder *= 0.7;
Encoder += Encoder_Least*0.3;
4、平均滤波程序设计
采用算术平均滤波法,即连续取N个采样值进行算术平均运算,通过加入算数平均滤波进而对一般具有随机干扰的信号进行滤波。
float filter2(float New_Value1)
{
static float filter_buf[20];
float filter_sum;
filter_buf[0] = New_Value1;
for(int i = 0; i < 20; i++)
{
filter_buf = filter_buf[i + 1];
filter_sum += filter_buf;
}
return filter_sum*0.05;
}五、PID程序设计
1、 单闭环PID
根据第一章的分析,我们直立环的程序如下:
int Banlance_PID(float Angle,float Mechanical_balance,float Gyro)
{
float Bias;
int out;
Bias = Angle - Mechanical_balance;
out = PID_Banlance.Kp*Bias+PID_Banlance.Kd*Gyro;
return out;
}
- 此函数三个入口参数分别为角度值,机械中值和角速度值,机械中值的获得会在后面介绍。
速度环程序如下:
int Velocity_PID(int Encoder_Left,int Encoder_Right)
{
static float out,Encoder_Least,Encoder;
static float Encoder_Integral;
Encoder_Least =(Encoder_Left+Encoder_Right)-0;
Encoder *= 0.7;
Encoder += Encoder_Least*0.3;
Encoder_Integral +=Encoder;
Encoder_Integral=Encoder_Integral;
if(Encoder_Integral>10000) Encoder_Integral=10000;
if(Encoder_Integral<-10000) Encoder_Integral=-10000;
out=Encoder*PID_Velocity.Kp+Encoder_Integral*PID_Velocity.Ki;
if(__fabs(Angle_Y)>60) Encoder_Integral=0;
return out;
}
2、抗积分饱和
程序中10000是积分上限值,当Encoder_Integral>10000时,取Encoder_Integral=10000,10000是积分的上限值,当Encoder_Integral<-10000时,取Encoder_Integral=-10000,-10000是积分的下限值,这样做是为了防止积分饱和,这种方法叫做“积分限幅法”;因为实际的执行器只能在一定的输入范围内有效,所以PID控制器的输出幅度需要限制。
if(Encoder_Integral>10000) Encoder_Integral=10000;
if(Encoder_Integral<-10000) Encoder_Integral=-10000; 3、串级PID
通过第一章的推导,输出方程可以将串级PID的算法转化成为:一个单独的负反馈的直立环 + 一个单独的正反馈的速度环。
Velocity_Pwm=Velocity_PID(enc1,enc2);
Balance_Pwm=Banlance_PID(Angle_Y,-2,Velocity_Angle_Y);
Turn_Pwm =Angle_Z*30;
Moto1=Balance_Pwm-Velocity_Pwm-Turn_Pwm;
Moto2=Balance_Pwm-Velocity_Pwm+Turn_Pwm;六、参数整定及极性判断
1、机械中值
由于小车结构的问题,小车的重心不一定与0角度在一条直线上,所以我们需要找到让重心平衡的角度,即机械中值。 首先,把小车放在地面上,从前向后以及从后向前绕电机轴旋转平衡小车,两次向另一边倒下的角度的中值,即为机械中值。
(举例:往后倒在2度,往后倒在-3度左右,本系统的机械中值为-1度。)
2、直立环:
- 极性错误:小车往哪边倒,车轮就往反方向开,会使得小车加速倒下。
- 极性正确:小车往哪边倒,车轮就往哪边开,以保证小车有直立的趋势。
<li data-pid="lNWZhQhF">Kp大小:
- Kp一直增加,直到出现大幅低频振荡。(即小车平衡时出现抖动)
<li data-pid="H9C7A6bs">Kd极性:
- 极性错误:拿起小车绕电机轴旋转,车轮反向转动,无跟随。
- 极性正确:拿起小车绕电机轴旋转,车轮同向转动,有跟随。
<li data-pid="MZumLNFt">Kd大小:
- Kd一直增加,直到出现高频振荡。(即触碰小车出现剧烈抖动)
直立环调试完毕后,对所有确立的参数乘以0.6作为最终参数。
- 原因:之前得到的参数都是Kp、Kd最大值,根据工程经验平衡小车的理想参数为最大参数乘以0.6求得。
- 结果:乘0.6后,小车抖动消失,但同时直立效果也变差。待下面加入速度环就能得到更好的性能。
3、速度环:
线性关系:Ki=(1/200)*Kp,仅调Kp即可。
- 在调节【速度环参数极性】时,需要去掉【直立环运算】
- 极性错误:手动转动其中一个车轮,另一车轮会以同样速度反向旋转——典型负反馈。
- 极性正确:手动转动其中一个车轮,两个车轮会同向加速,直至电机最大速度——典型正反馈。
<li data-pid="YYflgTIn">Kp、Ki大小:
- 增加Kp&Ki,直至:小车保持平衡的同时,速度接近于0,且回位效果好。
七、结束语
本文介绍了两轮平衡小车系统的总体设计方案,并从主控制器、检测环节、电机驱动等方面介绍了系统的主要硬件组成。针对多变量、强耦合、高度不稳定,非线性的两轮平衡小 车控制问题进行了研究,采用PID 控制算法对其进行控制,直立环采用 PD 控制的两轮其中 P 控制起主要作用,消除角度偏差、D 控制作用于系统过于激烈的情况,降低系统 超调。速度环采用 PI 控制算法,速度环补偿了角度环控制的不足, I 调节作为主要控制,通过对偏差值积分,提高了整个系统控制精度。最后搭建了两轮平衡小车样机,并利用试凑法整定了相关的 PID 参数,通过系统的软硬件设计、调试及运行情况,验证了PID 控制算法的有效性,使小车能够稳定地实现平衡控制。
<hr/>终于写完了,我滴妈, @知乎 咱能不能好好弄弄这个MarkDown导入的功能,导入完一团糟。
里面可能有些格式问题,如果遇到记得提醒我哈,需要全部代码可以私信或者评论找我哈。 |
|